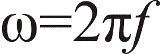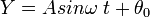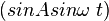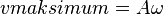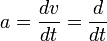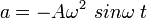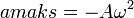Gerak Harmonik Sederhana : Makalah, Pengertian, Teori, Contoh

Oleh Diposting pada

Gerak Harmonik Sederhana

Gerak Harmonik Sederhana

Gerak Harmonik Sederhana – Apa itu yang di maksud dengan gerak harmonik sederhana? Nah, Berikut ini adalah materi makalah pengertian dan teori mengenai gerak harmonik sederhana, Jadi, Simaklah Penjelasannya di bawah ini.

Gerak Harmonik Sederhana

Pengertian Gerak Harmonik Sederhana

Gerak Harmonik Sederhana adalah gerak bolak balik secara teratur melalui titik keseimbangannya dengan banyaknya getaran benda dalam setiap sekon selalu sama atau konstan. Jika gerak yang terjadi secara berulang dalam selang waktu yang sama disebut gerak periodik.
Jika gerak ini terjadi secara teratur maka disebut juga sebagai gerak harmonik. Ketika suatu partikel melakukan gerak periodik pada lintasan yang sama maka geraknya disebut gerak osilasi/getaran. Bentuk sederhana dari gerak periodik adalah benda yang berosilasi pada ujung pegas. Karenanya kita menyebutnya gerak harmonis sederhana.

Jika dibuatkan grafik, gerak harmonis akan membentuk grafik sinus atau sinusoidal seperti berikut:

grafik sinusoidal gerak harmonik
Pada gerak harmonik terdapat beberapa besaran fisika yang dimiliki benda diantaranya:
  • Simpangan (y): jarak benda dari titik keseimbangan
  • Amplitudo (A): simpangan maksimum atau jarak terjauh
  • frekuensi (f): banyaknya getaran setaip waktu
  • Perioda (T):banyaknya waktu dalam satu getaran

Contoh Aplikasi Gerak Harmonik Sederhana

Biasanya dijelaskan pada kasus Ayunan Bandul dan Pegas

  • Gerak Harmonik Pada Bandul

Gerak Harmonik Pada Bandul

Persamaan:

Gerak Harmonik Sederhana
Gerak Harmonik Sederhana

Pada ayunan bandul sederhana, periode ayunan tergantung dari panjang tali dan gravitasi. Semakin besar panjang tali maka makin besar juga periodanya. Seperti persamaan berikut:

Perioda Ayuna Bandul

Keterangan:
T = Perioda (s)
l = Panjang tali (m)
g = percepatan gravitasi (m/s2)

Bandul sederhana atau pegas biasanya kita pergunakan untuk menentukan nilai percepatan gravitasi bumi dalam praktikum.

  • Gerak Harmonik Pada Pegas

Gerak Harmonik Pada Pegas

Untuk pegas nilai periodanya ditentukan menggunakan rumus berikut:
periode pegasKeterangan:
T = Perioda (s)
m = massa beban (kg)
K = konstanta pegas (N/m)

Apabila pegas perioda dipengaruhi oleh massa beban dan nilai konstanta pegas. Semakin besar massa beban maka makin besar nilai periodanya. Beda halnya dengan konstanta pegas, semakin besar konstanta pegas maka makin kecil nilai periodanya.

Animasi:

                                                         Gerak Harmonik Pada Pegas

Persamaan Simpangan dan Kecepatan serta Percepatan Getar Gerak Harmonis Sederhana.
  • Persamaan Simpangan Getar:

simpanan getar

Keterangan :
Y = simpangan (m)
A = simpangan maksimum (amplitudo) (m)
f = frekuensi (Hz)
t = waktu (s)

\omega = kecepatan sudut (rad/s)

kecepatan sudut

Jika posisi sudut awal adalah \theta_0, maka persamaan gerak harmonik sederhana menjadi:

peramaan gerak harmonik

  • Kecepatan Gerak Harmonik Sederhana

Dari persamaan gerak harmonik sederhana peramaan gerak harmonik

Kecepatan gerak harmonik sederhana :
v = \frac{dy}{dt} (sin A sin \omega\ t)

v = A \omega\ cos \omega\ t

Kecepatan maksimum dapat diperoleh jika nilai cos \omega\ t = 1 atau \omega\ t = 0, sehingga :

v maksimum = A \omega

  • Kecepatan untuk Berbagai Simpangan

Y = A sin \omega\ t.
Persamaan tersebut dikuadratkan

Y^2 = A^2 sin^2 \omega\ t, maka :

Y^2 = A^2 (1 - COS^2 \omega\ t)

Y^2 = A^2 - A^2 COS^2 \omega\ t …(1)

Darii Persamaan : v = A \omega\ cos \omega\ t
\frac{v}{\omega} = A cos \omega\ t …(2)

Persamaan (1) dan (2) dikalikan, sehingga didapatkan :
v^2 = \omega\ (A^2 - Y^2)

Keterangan :
v = kecepatan benda pada simpangan tertentu (m/s)
\omega = kecepatan sudut (rad/s)
A = amplitudo (m)
Y = simpangan (m)

  • Percepatan Gerak Harmonik Sederhana

Dari persamaan kecepatan yakni : v = A \omega\ cos \omega\ t, maka :
a = \frac{dv}{dt} = \frac{d}{dt}
a = -A \omega^2\ sin \omega\ t
Percepatan maksimal jika \omega\ t = 1 atau \omega\ t = 900 = \frac \pi 2
a maks = -A \omega^2\ sin \frac \pi 2
a maks = -A \omega^2\

Note:
Dilihat dari Persamaan diatas dapat disimpulkan bahwa dalam gerak harmonis, percepatan getar benda berbanding lurus dengan simpangannya. semakin besar simpangannya maka semakin besar pula percepatannya.

Keterangan :
a maks = percepatan maksimum (m/s2)
A = amplitudo (m)
= kecepatan sudut (rad/s)

Energi Gerak Harmonik

sebuah benda yang bergerak harmonik memiliki energi potensial dan energi kinetik. Jumlah kedua energi ini disebut energi mekanik.

a. Energi Potensial Gerak Harmonik

Energi potensial bisa dirumuskan atas dasar perubahan gaya yang bekerja pada gerak harmonik. Energi potensial berbanding lurus dengan simpangannya (F = ky). Energi potensial gerak harmonik dirumuskan sebagai berikut.

Apabila diuraikan, energy potensial menjadi

15ab

Energy potensial maksimum jika nilai sin2 ωt=1, ketika benda berada pada simpangan maksimum, kecepatan benda = 0.

16ab

b. Energi Kinetik Gerak Harmonik

Energi kinetik gerak harmonik dirumuskan sebagai berikut.

17ab

Energy kinetic maksimum dicapai benda pada titik seimbangnya. Energy kinetic minimum dapat dicapai benda pada simpangan maksimum (titik balik). Energy kinetic maksimum dirumuskan sebagai berikut.

18ab

c. Energi Mekanik

Energi mekanik yang terjadi pada benda yang bergetar harmonik tidak bergantung waktu dan tempat sehingga energi mekanik yang terjadi pada benda- di mana pun adalah sama.

19ab

Demikianlah Ulasan kami mengenai Gerak Harmonik Sederhana, Semoga bermanfaat…

Refrensi Teknologi : KLIKDISINI 

Posting terkait: