Rumus Kinematika

Pada kesempatan kali ini kita akan belajar bersama mengenai kinematika

Kinematika sendiri dibagi menjadi tiga.

Apa saja itu? Mari kita simak bersama.

Pengertian Kinematika

Kinematika merupakan bagian dari ilmu fisika yang membahas tentang gerak. Terus bagaimana bisa benda dikatakan bergerak?

Jawabannya adalah jika benda tersebut mengalami perpindahan posisi. Lantas jika benda berpindah posisi dalam waktu tertentu disebut apa?

Kalau perpindahan posisidalam waktu tertentu kita sebut dengan kecepatan. Lantas kita kecepatan itu berubah ubah disetiap waktu kita sebut dengan percepatan.

Posisi, kecepatan, dan percepatan adalah besaran dalam fisika yang memiliki hubungan erat dengan kinematika ini.

Besaran besaran ini merupakan besaran vector yang mana memiliki besar dan arah. Kinematika sendiri memiliki beberapa jenis yaitu kinematika gerak dan dinematika partikel.

Mari kita bahas satu persatu di sub bab berikutnya.

Kinematika Partikel

Pada kinematika partikel saya mau meluruskan dulu ya. Partikel yang dibahas disini nukan dilihat dari ukuran akan tetapi roket yang meluncur ke luar angkasa juga kita menyebutnya partikel di pembahasan ini.

Jadi secara singkat kinematika partikel merupakan ilmu yang mempelajari gerak benda dalam kesatuan utuh partikel.

Kita menyebutnya partikel karena benda tersebut bergerak dalam satu kesatuan yang utuh dan tidak mengalami putaran terhadap poros benda tersebut.

Kinematika Gerak

Kinematika gerak merupakan ilmu fisikayang mempelajari tentang gerak suatu benda dilihat secara makro atau besar.  Kinematika gerak sendiri terdapat beberapa jeni, antara lain:

Gerak Lurus Beraturan (GLB)

Gerak lurus beraturan adalah gerak suatu benda yang memiliki lintasan lurus.

Gerak ini memiliki ciri dimana percepatan yang dialami bernilai 0 karena padagerak lurus benda tersebut tidak mengalami perubahan kecepatan.

Untuk lebih memahaminya mari kita lihat ilustrasi dibawah ini.

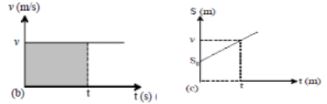
Pada gambar kiri kita dapat melihat hubungan kecepatan terhadap waktu. Di gambar tersebut telah digambarkan bahwa nilai kecepatan pada setiap waktu tidak mengalami perubahan.

Pada gambar kanan terlihat hubungan antara posisi dengan waktu  dimana terlihat  grafiknya adalah lurus keatas.

Gerak Lurus Berubah Beraturan (GLBB)

Pada kejadian ini kita sering mengamatinya saat kita memegang stuatu barang dan tanpa sengaja kita menjatuhkannya dari genggaman kita.

Di situlah GLBB bekerja. GLBB merupakan gerak dimana benda mengalami percepatan yang tetap.

Sebenarnya Gerak lurus berubah beraturan (GLBB) dan Gerak jatuh bebas (GJB) merupakan gerak yang sama yang membedakan adalah arah geraknya.

GLBB memiliki arah gerak horizontal dan GJB memiliki arah gerak vertical. Berikut merupakan ilustrasi dari GLBB dan GJB.

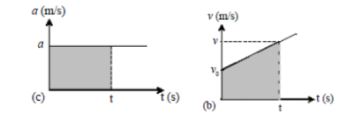
Padailustrasi diatas tergambarkan bahwa percepatan benda pada setiap waktu konstan nilainya.

Pada gambar kanan juga menjelaskan grafik hubungan kecepatan dan waktu dimana nilai kecepatan setiap waktu mengalami kenaikan tergambar dari grafik kecepatan menukik ke atas.

Setelah kita dapat memahami  pengertian dan materi kinematika partikel dan kinematika gerak maka kita akan membahas persamaan matematis  supaya dapat menyelesaikan masalah masalah yang ada dalam topik kinematika sendiri.

Rumus Kinematika

Persamaan kinematika dapat diselesaikan jika kalian telah memahamikonsepkonsep dasar persamaan ini. Untuk memahaminya mari kita simak dengan seksama.

Rumus Kecepatan

V = x/t

Rumus Percepatan

a = ∆V/∆t = (V₂-V₁)/(t₂-t₁)

Kinematika Gerak

• Kinematika posisi

x = v₀t ± ½ at²

• Kinematika kecepatan

v_t = v₀ ± at

V_t² = V₀² ± 2ax

Dimana

• V = kecepatan (m/s)
• x = posisi (m)
• t = waktu (s)
• a = percepatan (m/s²)
• v₂ = kecepatan sesudah (m/s)
• v₁ = kecepatan sebelum (m/s)
• t₂ = waktu sesudah (s)
• t₁ = waktu sebelum (s)
• v₀ = kecepatan awal (m/s)
• v_t = kecepatan ahir padawaktu tertentu (m/s)

Setelah memahami persamaan yang digunakan dan telah mempelajari materi yang telah dijelaskan untuk menguji daya tangkap maupun pemahaman kalian mari kita kerjakan bebebrapa soal berikut ini.

Contoh Soal Kinematika

Setelah 6 s dari keadaan diam, kecepatan benda menjadi 4 m/s. Kemudian, benda bergerak dengan kecepatan konstan. Waktu total, dari waktu diam, yang dibutuhkan benda untuk mencapai jarak total 20 m adalah …..

Demikian pembahasan dari PPKN.CO.ID tentang rumus kinematika. Semoga bermanfaat

Refrensi Teknplogi : KLIKDISINI