Contoh Gerak Parabola

Holaaa temen-temen semangat pagi, di artikel kali ini kita akan membahas tentang gerak parabola. Simak penjelasannya..
Pengertian Gerak Parabola
Temen-temen pasti sudah tidak asing dengan istilah parabola, apa yang terlintas di benak kalian ketika mendengar kata parabola?
Kalian membayangkan sesuatu yang seperti mangkok dan biasanya terdapat pada atap rumah kah?
Jadi, yang akan kita bahas kali ini adalah gerak parabola, gerak yang merupakan perpaduan antara gerak lurus beraturan (GLB) dan gerak lurus berubah bertauran (GLBB).
Bila kalian membayangkan parabola tv sebenarnya ada kesamaan dengan gerak parabola, yaitu lintasan gerak parabola melengkung mirip parabola tv namun tidak penuh.
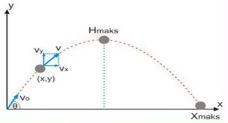
Gerak parabola ini diberi kecepatan awal, dan untuk gerak benda sepenuhnya dipengaruhi oleh gaya gravitasi. Gerak parabola diuraikan dalam 2 arah, yaitu arah vertical dana arah horizontal.
Arah vertical yang dipengaruhi gaya gravitasi menyebabkan GLBB dana rah horizontal benda merupakan GLB.
Nah temen-temen untuk penulisan gerak parabola secara sistematisnya dapat kalian simak di poin selanjutnya, okk.
Rumus Gerak Parabola
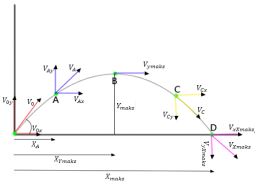
Rumus gerak parabola diuraikan dalam 2 sumbu. Untuk rumus gerak parabola pada sumbu x maka diuraikan sebagai berikut :
vx = v0x = v0 cos α
x = vxt = v0 cos α t
dimana
- vx = kecepatan akhir benda pada sumbu x (m/s) ;
- v0 = kecepatan awal benda (m/s)
- α = sudut elevasi yang terbentu antara sumbu x dengan lintasan
- t = waktu yang dibutuhkan untuk menempuh lintasan parabola
sedangkan untuk penuisan sistematis yang diuraikan pada sumbu y sebagai berikut :
gerak secara vertikal akan dipengaruhi oleh gaya gravitasi.
vy = v0y – gt
bila ditinjau pada sumbu vertika v0y = v0 sin α, maka
vy = v0 sin α – gt
untuk penguraian gerak parabola pada sumbu y, maka bisa diketahui posisi benda sebagai berikut :
y = v0y t – ½ gt2
atau
y = v0 sin α t – ½ gt2
dimana
- vy = kecepatan akhir benda pada sumbu y (m/s) ;
- v0y = kecepatan awal benda (m/s)
- α = sudut elevasi yang terbentu antara sumbu x dengan lintasan
- t = waktu yang dibutuhkan untuk menempuh lintasan parabola
Beberapa persamaan khusus pada materi gerak parabola sebagai berikut :
- Kecepatan benda dalam gerak parabola yang diuraikan pada komponene sumbu0x dan sumbu-y dapat dituliskan sebagai berikut :
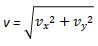
- Arah benda gerak parabola pada komponen sumbu-x bisa dituliskan sebagai berikut :
tan θ = vy / vx
sehingga nilai vx selalu positif namun juga bergantung pada nilai vy
- Pada komponen sumbu-y, benda akan memiliki kecepatan = 0 ketika benda pada posisi tinggi maksimum, sehingga penulisan sistematisnya sebagai berikut :
tAB = (v0 sinα)/ g
- Tinggi maksimum benda pada komponen sumbu-x, yakni :
H =( v02 sin2α)/2g
- Jarak tempuh maksimum benda pada komponen sumbu-x, yakni
X =v0xtAC = v0cosα 2(v0 sinα/g) = v022 (sinα/g) cos α
X =( v02 sin 2α)/g
Supaya temen-temen jauh lebih paham, simak contoh soalnya yaa..
Gerak Parabola Dalam Kehidupan Sehari-hari
Dalam kehidupan sehari-hari sebenarnya mudah untuk kita menemui gerak parabola. Misalnya seperti :
- Menendang bola yang semula diam dengan punggung kaki .
- Melesatkan peluru atau batu yang dipasang pada ketapel.
- Shooting yang dilakukan oleh pemain bola basket.
- Ketika menerbangkan pesawat yang terbuat dari kertas lipat, dan masih banyak lagi.
Okey, supaya temen-temen lebih faham tentang penjelasan dari gerak parabola simak contoh soalnya yahh..
Contoh Soal Gerak Parabola
Bola ditendang oleh seorang pemain sepakbola, kecepatan awal bola tersebut 20 m/s, sudut elevasi yang terebentuk antara lintasan bola dengan sumbu x yakni 370 (sin 370 = 0,6). Dan percepatan gravitasinya sebesar 10 m/s2, hitunglah tinggi maksimum dan jarak maksimum yang dapat dicapai oleh bola tersebut
Diketahui
v0 = 20 m/s ; α = 370
H =( v02 sin2α)/2g
H = (202 sin 2 370)/2.10
H = (202 (0,6) 2)/2.10
H = 7,2 m
X = ( v02 sin 2α)/g
X = (202 2(sin 370 cos 370))/10
X = 38,4 m
Maka, tinggi maksimum yang dapat dicapai oleh bola yaitu 7,2m dan jarak terjauh yang dapat dicapai bola yaitu 38,4 m.
Demikian pemaparan materi dari PPKN.CO.ID semoga bisa bermanfaat dan menambah semangat temen-temen untuk terus belajar dan berkarya.aamiin.
Refrensi Teknologi : DISINI