Contoh Soal Matriks

Contoh Soal Matriks – Pada Kesempatan kali ini PPKN.CO.ID tentu seperti tujuan sebelumnya penulis akan berbagi berbagai artikel bermanfaat untuk kita semua. Kali ini penulis membawa sebuah artikel dengan pembahasan Contoh Soal Matriks. Berikut pembahasan terlengkapnya yang dapat sobat pahami.
Pengertian Matriks
Matriks adalah suatu kumpulan dari bilangan yang bisa disusun dengan berbagai baris atau secara kolom atau dapat juga disusun dengan bentuk kedua – duanya dan dapat di apit dalam bentuk tanda kurung. Elemen – elemen dari matriks terdiri dari berbagai bilangan – bilangan tertentu yang akan membentuk di dalam sebuah matriks.
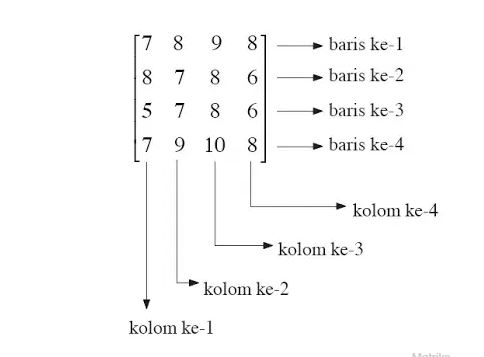
Operasi Aljabar Pada Matriks
Matriks adalah berbagai susunan bilangan-bilangan yang akan dinyatakan dalam baris serta kolom
Penjumlahan dengan pengurangan matriks
Dua buah matriks bisa dijumlahkan atau bisa dikurangi apabila mempunyai ordo yang sama. Caranya yaitu dengan cara menjumlahkan atau dengan cara mengurangi elemen seletak,
Contoh:
Diketahui berbagai matriks-matriks berikut:
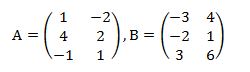
Tentukan:
A + B
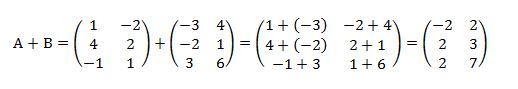
Macam – Macam Matriks
Matriks mempunyai macam – macamnya, yaitu antara lain :
Matriks Baris
Matriks Baris adalah sebuah matriks yang hanya akan terdiri dari satu baris saja tanpa adanya kumpulan kolom yang terdapat di dalamnya.
Contoh :
A = [3 2 1]
B = [4 5 – 2 5]
Matriks Kolom
Matriks Kolom ialah matriks yang hanya terdiri dari satu kolom saja tanpa adanya kumpulan baris di dalamnya.
Contoh :
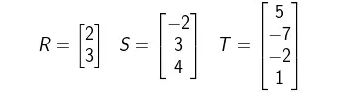
Matriks Persegi
Matriks Persegi adalah matriks yang banyak mempunyai baris sama dengan jumlah dari banyak kumpulan kolom dari satu matriks.
Contoh :

Matriks Diagonal
Matriks Diagonal adalah matriks persegi dengan bagian setiap elemen yang bukan hanya elemen – elemen diagonal yang merupakan utamanya ialah 0 (nol), sedangkan dari elemen dalam diagonal yang paling utamanya tidak seluruhnya nol.
Contoh :
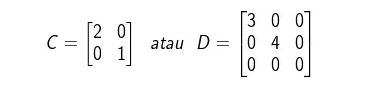
Matriks Identitas
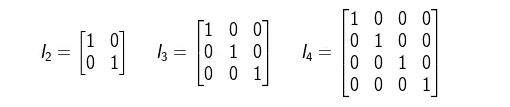
Matriks Identitas adalah matriks dengan persegi dengan seluruh elemen pada diagonal utama ialah 1 (satu) dengan elemen lainnya semuanya bernilai 0 (nol). Pada umumnya matriks identitas bisa dinotasikan dengan I apabila disertai dengan ordonya.
Contoh :
Matriks Nol
Matriks Nol yaitu sebuah matriks yang dimana seluruh elemennya ialah 0 (nol). Matriks nol yang biasanya dinotasikan bersama huruf O diikuti dengan ordonya, Om x n.
Contoh :

Jenis Matriks
Berikut dibawah ini merupakan berbagai jenis matriks, antara lain.
Transpos Matriks
Matriks A transpos (At) adalah bentuk matriks yang telah disusun dengan cara menuliskan baris ke-i dengan matriks A menjadi kolom ke–i serta sebaliknya.
Contoh:
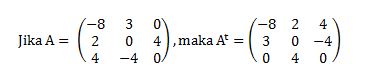
Beberapa sifat dari matriks adalah sebagai berikut ini.
- (A + B)t= At + Bt
- (At)t= A
- (cA)t= cAt, c merupakan konstanta
- (AB)t= BtAt
Determinan
Determinan dari bentuk matriks A dinotasikan dengan lambang |A|
Jika memiliki ordo 2×2, cara menentukan determinannya:
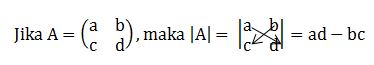
Jika memiliki ordo 3×3 menggunakan kaidah dari Sarrus

Invers Matriks
Invers dari bentuk matriks A dinotasikan dengan lambang A-1
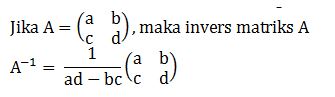
Syarat matriks A harus mempunyai invers.
- Jika |A| = 0, maka matriks A tidak akan mempunyai invers. Oleh sebab itu, dikatakan apabila matriks A sebagai bentuk matriks singular.
- Jika A ≠ 0, maka nilai matriks A mempunyai bentuk invers. Oleh karena itu, dikatakan bentul matriks A sebagai matriks yang merupakan matriks nonsingular.
Penerapan Matriks dalam Sistem Persamaan Linear
Jika ada sevuah sistem persamaan linear sebagai berikut.
ax + by = e
cx + dy = f
Sistem dari persamaan linear tersebut bisa kita tuliskan dalam bentuk persamaan matriks sebagai berikut.
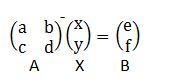
Persamaan matriks ini bisa kita selesaikan dengan cara menggunakan sifat
berikut.
- Jika AX = B, maka di dapat X A-1B, dengan bentuk |A| ≠ 0
- Jika XA = B, maka bisa di dapat X = BA-1, dengan bentuk |A| ≠ 0
Contoh Soal Matriks
Dibawah ini akan dibahas contoh soal matriks invers, matriks bentuk perkalian, dan matriks dari transpose, penjumlahan, dan serta bentuk pengurangan beserta pembahasan dengan jawabannya…
- Diketahui
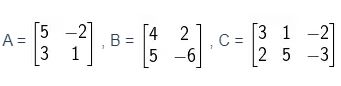 Tentukan :
Tentukan :
- A + B :
- A + C :
Penyelesaian :

- Jika gambar 9 adalah =….
Penyelesaian :
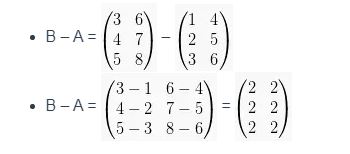
Sifat dari matriks penjumlahan dan pengurangan dalam suatu matriks yaitu :
- A + B = B + A
- (A + B) + C = A + (B + C)
- A – B ≠ B – A
- Jika matriks telah saling invers, tentukan berapa nilai x !
Penyelesaian :
Diketahui bahwa dari kedua matriks diatas tersebut telah saling invers, maka berlaku syarat dimana AA-1 = A-1A = I.
Maka :
Sehingga dalam elemen baris ke-1dalam kolom ke-1 memiliki berbagai persamaan yaitu :
-
- 9(x -1) – 7x = 1
- 9x – 9 – 7x = 1
- 2x = 10
- x = 5
Jadi, nilai x ialah = 5
- Diketahui
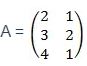 , Tentukan berapa nilai dari 3A !
, Tentukan berapa nilai dari 3A !
Penyelesaian :

Demikianlah pemabahasan mengenai tentang Contoh Soal Matriks. Semoga dipermudah dalam memahami materi serta dapat membantu sobat dalam menyelesaikan tugas, belajar ujian dan lain sebagainya. Sekian artikel ini penulis bagikan sampai jumpa dilain kesempatan.
Refrensi Teknologi : KLIKDISINI