Rumus Matematika Kelas 6 Semester 1

Rumus Matematika Kelas 6 SD – Pada kesempatan ini PPKN.CO.ID hadir dengan memberikan sebuah artikel yang kali ini mengenai tentang Rumus Matematika Kelas 6 SD. Nah untuk sobat yang penasaran dengan pembahasan yang lengkap, bisa sobat simak dibawah ini.

Kumpulan Rumus Matematika Kelas 6 SD

Berikut dibawah ini merupakan kumpulan berbagai rumus matematika yang bisa sobat pahami dan pelajari, antara lain.

Rumus Matematika Hitung Volume Bangun Ruang

Nama Bangun Ruang	Rumus Volume
Tabung	V = phi r² x t
Prima tegak segitiga	V = Luas alas x Tinggi

Kumpulan Rumus Hitung Skala

Rumus Skala	= Jarak dalam Gambar (Peta) atau Jarak Sebenarnya
Rumus Jarak Pada Gambar	= Jarak Sebenarnya x Skala
Rumus Jarak Sebenarnya	= Jarak di Gambar (Peta) atau Skala

Kumpulan Rumus Luas Bangun Datar

Bangun Datar	Rumus Luas
Persegi	L = s x s = s²
Segitiga	L = ½ a x t
Lingkaran	L = phi x r²
Trapesium	L = ½ t × (a+b)
Layang – Layang	L = ½ x d1 x d2
Jajar Genjang	L = A x T
Belah Ketupat	L = 1/2 x d1 x d2
Persegi Panjang	L = P x L

Rumus Operasi Bilangan Bulat

• Ada Sifat Komutatif dari Penjumlahan, Rumus dengan Bentuk Umum : a + b = b + a

Contohnya : 3 + 4 = 4 + 3 = 7 atau 5 + 6 = 6 + 5 = 11

• Jenis Sifat komutatif dari Perkalian, Rumus dari Bentuk Umum : a x b = b x a

Contohnya : 2 x 5 = 5 x 2 = 10 atau 6 x 2 = 2 x 6 = 12

• Selanjutnya Sifat Distributif dari Perkalian terhadap hitungan Penjumlahan

Bentuk Rumus Umumnya : a x (b + c) = (a x b) + (a x c)

Contohnya :

2 x (52 + 10)	= 2 x 2 + 2 x 10
	= 4 + 20
	= 24

• Sifat Distributif dari Perkalian terhadap hitungan Pengurangan

Bentuk Rumus Umumnya : a x (b – c) = (a x b) – (a x c)

Contohnya :

2 x (5 – 5)	= 2 x 5 – 2 x 5
	= 10 + 10
	= 20

Kumpulan Rumus Operasi Hitung Bilangan Campuran

Operasi Hitung dari Bilangan Campuran mempunyai 2 Ketentuan, sebagai berikut :

Pertama apabila terdapat tanda kurung (), maka yang akan di kerjakan di dalam tanda kurung itu terlebih dahulu.

Kedua apabila tidak ada tanda kurung (), maka yang pertama dikerjakan Perkalian & Pembagian yang terlebih dahulu, setelah itu baru bisa di kerjakan Penjumlahan & Pengurangannya.

Contoh :

= 6000 – 40 x 100 : 4 + 200		= 2000 : 10 x 2 – (200 + 50)
= 6000 – 1000 + 200		= 2000 : 10 x 2 – 150
= 5200	Atau	= 200 x 2 – 150
		= 400 – 150
		= 250

Rumus FPB dan KPK  Dua Bilangan

Cara Menentukan nilai FPB Dua Bilang sebagai berikut dengan  Cari Faktor di masing masing bilangan yang tersebut, Contohnya :

8	= 2³
18	= 2 x 4²

Faktor yang sama dari nilai FPB yang ada pada Dua Bilangan tersebut adalah 3, dan yang berpangkat dinilai paling kecil ialah 2³ = 8

Cara untuk Menentukan KPK Dua Bilangan dengan mencari Faktor Prima berdasarkan Masing – Masing angka Bilangan tersebut, kalikan seluruh faktor dengan faktor yang sama maka selanjutnya dipilih pangkat yang nilainya paling tinggi.

Contohnya : Nilai KPK 12 dan 15

12	= 2² x 3
15	= 3 x 5

Nilai KPK Dua Bilangan diatas ialah : 2² x 3 x 5 = 50

Mengolah dan Menyajikan Data

Modus merupakan Nilai yang paling banyak akan muncul.

Nilai Minimum ialah Nilai yang terkecil serta yang terendah dari seluruh data.

Nilai Maksimal merupakan Nilai yang tertinggi dari seluruh data yang ada didalamnya.

Rata – Rata ialah Untuk Rata – Rata yang akan dicari dengan cara mereka menjumlahkan seluruh Sampel yang akan dibagi dengan Jumlah Sampel.

• Mencari Sistem Koordinat
• Sumbu x juga akan disebut dengan Absis (x) dan untuk keterangan Sumbu y disebut dengan Ordinat (y).
• Suatu bidang Koordinat Cartesius akan dapat terbentuk oleh 2 Buah Sumbu yaitu Sumbu Tegak (Sumbu y) dengan Sumbu Mendatar (Sumbu x).
• Dari titik Nol Sumbu tegak yang akan menukik ke Atas dan Sumbu Mendatar yang akan lebih ke Kanan yang memiliki Nilai Positif.
• Dari Titik Nol Sumbu Tegak akan menukik ke Bawah dengan Sumbu Mendatar akan ke Kiri yang memiliki Nilai Negatif.
• Mencari titik Koordinat sebuah Objek yang dapat dicari dengan cara mencari letak di Sumbu x ke Kanan serta ke Kiri dengan letak Sumbu y ke Atas serta ke Bawah.

Hubungan Satuan Volume

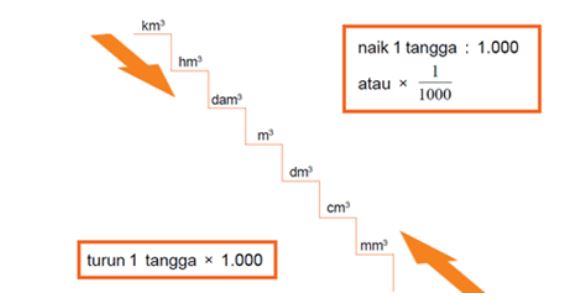
Contoh :

1 km³ = 1.000 hm³ (turun 1 tangga)

1 m³ = 1.000.000 cm³ (turun 2 tangga)

1 m³ =1/1.000 dam³ (naik 1 tangga)

1 m³ = 1/1.000.000 hm³ (naik 2 tangga)

Volume dalam Liter

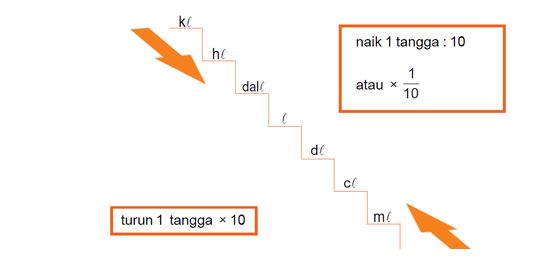
Satuan Waktu

Satu Menit	= 60 Detik
Satu Jam	= 60 Menit
Satu Hari	= 24 Jam
Satu Minggu	= 7 Hari
Satu Bulan	= 30 Hari / 31 Hari
Satu Bulan	= 4 Minggu
Satu Tahun	= 52 Minggu
Satu Tahun	= 12 Bulan
Satu Windu	= 8 Tahun
Satu Dekade	= 10 Tahun
Satu Dasawarsa	= 10 Tahun
Satu Abad	= 100 Tahun
Satu Milenium	= 1000 Tahun

Konversi Detik

• 1 menit = 60 detik
• 1 jam = 3 600
• 1 hari = 86 400
• 1 bulan = 2 592 000 detik
• 1 tahun = 31 104 000 detik

Penjumlahan dan Pengurangan Pecahan

Untuk bisa menambah serta mengurangkan pecahan yang pertama terlebih dahulu samakan penyebutnya.

Contoh:

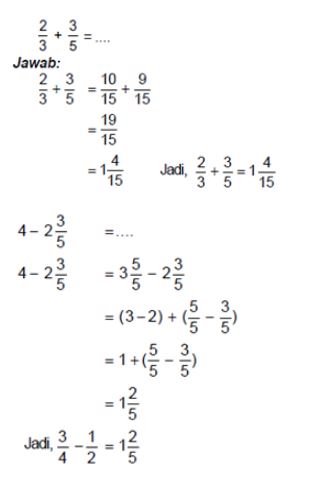
Mengalikan dan Membagi Pecahan

Mengalikan pecahan ini dengan cukup mudah. Pembilang dikalikan dari pembilang. Penyebut yang dikalikan dengan penyebut. Jika bisa juga disederhanakan maka sederhanakanlah:

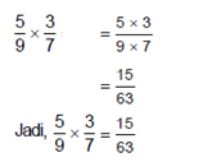
Pembagian pecahan yang sama dengan mengalikan kebalikan bilangan pecahan dengan pembagi.

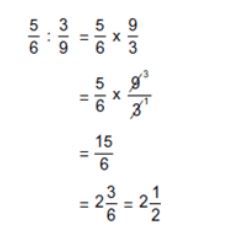
Menentukan Akar Pangkat 3 Bilangan Kubik

1³  = 1 × 1 × 1 = 1
2³  = 2 × 2 × 2 = 8
3³  = 3 × 3 × 3 = 27
4³  = 4 × 4 × 4 = 64
5³  = 5 × 5 × 5 = 125

1, 8, 27, 64, 125, seterusnya merupakan bilangan kubik atau dengan bilangan pangkat 3

Penjumlahan dan Pengurangan

2³ + 1³ = (2 × 2 × 2) + (1 × 1 × 1)
= 8 + 1
= 9

6³ – 5³ = (6 × 6 × 6) – (5× 5 × 5)
= 216 – 125
= 91

Perkalian dan Pembagian

2³ × 7³ = (2 × 2 × 2) × (7 × 7 × 7)
= 8 × 343
= 2.744

4³ : 2³ = (4 × 4 × 4) : (2 × 2 × 2)
= 64 : 8
= 8

Demikianlah artikel dari PPKN.CO.ID  dengan pembahasan mengenai tentang Rumus Matematika Kelas 6 SD Semester 1. Semoga berbagai rumus diatas bisa membantu sobat untuk memahami dan menyelesaikan berbagai tugas matematika dengan mudah.

Refrensi Teknologi : KLIKDISINI