Limit Fungsi Trigonometri – Halo sobat PPKN.co.id di dalam pertemuan kali ini penulis akan berbagi sebuah artikel yang kali ini akan membahas tentang Limit Fungsi Trigonometri. Sering kali dalam mempelajari matematika kita semua sudah berfikir bahwa materi matematika ini akan sangat sulit dan tidak bisa kita pahami, nah tenang saja penulis punya solusinya yang pembahasan terlengkapnya sendiri bisa sobat simak berikut ini.

Pengertian Trigonometri
Trigonometri adalah sebuah cabang dari ilmu matematika yang akan mempelajari hubungan antara panjang serta sudut segitiga, biasanya akan digunakan dalam membuat desain bangunan, pembuatan jembatan serta pada bidang astronomi.
Sedangkan limit trigonometri ialah nilai paling dekat dari sebuah sudut. Istilah-istilah yang ada pada trigonometri yaitu sinus (sin), cosinus (cos), cosecan (csc), tangen (tan), secan (sec), dan cotangent (ctg).
Untuk menentukan nilai dari limitnya, berbagai cara/metode yang sering digunakan adalah substitusi, pemfaktoran, turunan, dan juga kali sekawan.
Dalam trigonometri, ada beberapa rumus yang akan terbentuk seperti di bawah ini
Rumus kebalikan
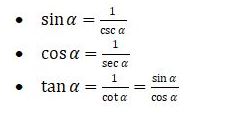
Rumus identitas

Rumus jumlah dan selisih trigonometri
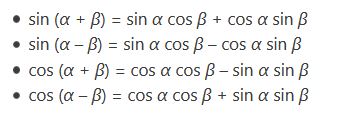
Rumus perkalian
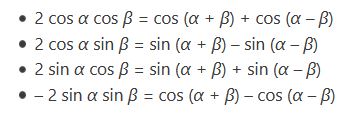
Sudut rangkap
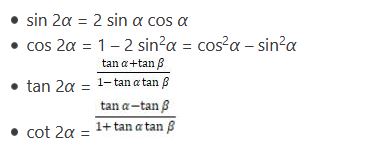
Turunan Trigonometri
Beriku merupakan tabel turunan dari trigonometri yang dapat dipelajari dan dipahami, yaitu.
| f (x) | f’(x) |
| sin x | cos x |
| cos x | – sin x |
| tan x | sec2 x |
| cot x | – csc2 x |
| sec x | sec x tan x |
| csc x | – csc x cot x |
Limit Fungsi Trigonometri
Sama halnya dengan pembahasan limit trigonometri, limit fungsi trigonometri adalah nilai paling dekat dari sebuah sudut pada fungsi trigonometri. Dalam kegiatan penghitungannya, terdapat 2 (dua) teorema yang akan menjadi dasar dari limit fungsi trigonometri seperti yang ada di bawah ini:
Teorema 1 (hanya berlaku pada saat x → 0)
Rumus dan ketentuan yang harus dipahami untuk mudah menginat dan mengerjakan soal, yaitu.
Teorema 2 (hanya berlaku pada saat x → c, Ɐc ∈ R)
Berikut rumus teorema 2 yang dapat sobat pahami dan pelajari, yaitu.
Sudut-sudut istimewa yang adadalam trigonometri yaitu 0o, 30o, 45o, 60o, 90o. Supaya lebih mudah dalam kegiatan memahami sudut istimewa, perhatikan juga tabel sudut istimewa dari 4 kuadran yang ada di bawah ini:
Kuadran 1
Adapun tabel kuadran 1 yang dapat sobat pelajrai selengkapnya berikut ini.
| 0o | 30o | 45o | 60o | 90o | |
| sin α | 0 | ½ | ½√2 | ½√3 | 1 |
| cos α | 1 | ½√3 | ½√2 | ½ | 0 |
| tan α | 0 | ⅓√3 | 1 | √3 | – |
| csc α | – | 2 | √2 | ⅔√3 | 1 |
| sec α | 1 | ⅔√3 | √2 | 2 | – |
| cot α | – | √3 | 1 | ⅓√3 | 0 |
Kuadran 2
Untuk kuadran 2 yang dapat di pelajari penulis sajikan berikut ini.
| 90o | 120o | 135o | 150o | 180o | |
| sin α | 1 | ½√3 | ½√2 | ½ | 0 |
| cos α | 0 | -½ | -½√2 | -½√3 | -1 |
| tan α | – | -√3 | -1 | -⅓√3 | 0 |
| csc α | 1 | ⅔√3 | √2 | 2 | – |
| sec α | – | – 2 | -√2 | -⅔√3 | -1 |
| cot α | 0 | -⅓√3 | -1 | -√3 | – |
Kuadran 3
Berikut dibawah ini merupakan tabel mengenai tentang kuadran 3 yang dapat di pelajari, yaitu.
| 180o | 210o | 225o | 240o | 270o | |
| sin α | 0 | -½ | -½√2 | -½√3 | -1 |
| cos α | -1 | -½√3 | -½√2 | -½ | 0 |
| tan α | 0 | ⅓√3 | 1 | √3 | – |
| csc α | – | -2 | -√2 | -⅔√3 | -1 |
| sec α | -1 | -⅔√3 | -√2 | – 2 | – |
| cot α | – | -√3 | 1 | -⅓√3 | 1 |
Kuadran 4
Adapun tabel kuadran 4 bisa sobat simak berikut ini.
| 270o | 300o | 315o | 330o | 360o | |
| sin α | -1 | -½√3 | -½√2 | -½ | 0 |
| cos α | 0 | ½ | ½√2 | ½√3 | 1 |
| tan α | – | -√3 | -1 | -⅓√3 | 0 |
| csc α | -1 | -⅔√3 | -√2 | -2 | – |
| sec α | – | 2 | √2 | ⅔√3 | -1 |
| cot α | 1 | -⅓√3 | -1 | -√3 | – |
Contoh Soal Limit Trigonometri
Berikut dibawah ini merupakan 3 contoh soal dan pembahasan limit trigonometri, yaitu.
Demikianlah artikel yang telah membahas Limit Fungsi Trigoometri. cukup mudah bukan untuk dipahami, selain belajar memahami materi matematika akan dpat dikuasi dengan memperbanyak latihan seperti memperbanyak megerjakan berbagai soal untuk emgasah kemampuan dan meningatkan pemahaman kita. Semoga dapat dengan mudah dipahami dan di aplikasikan dalam pembahasan tugas yang sobat miliki.
Baca Juga :
